Can You Divide By Zero?

A Mathematical Discussion

Readers may wonder why I don’t spend much time talking about physics. The answer isn’t that physics is boring, but physics is really hard to understand. People think physicists put on white coats and goggles and play around with interdimensional portals or something, but frankly the first episode of Big Bang Theory got it right when Leonard and Sheldon introduced Penny to the complicated scribbling on their whiteboards. That’s physics.

Now for better or worse, I personally spend my time among ordinary mortals. And with some regularity, these people keep insisting that they don’t want to go through my interdimensional portal “You can’t divide by zero.” This is wrong. It seems like not a day passes without somebody telling me something boring and wrong, and this is my life. I know, what they really mean to say when they talk to me is “No one can divide by zero,” but this is still wrong.

It’s only really accurate for them to say “I can’t divide by zero.” I’d believe them if they say that. That’s true. They can’t. But that’s a limitation I don’t share, and you don’t have to, either.

Now if you’re not interested in mathematics, I realize this may seem trivial, but scroll down, and you’ll see the consequences reach beyond mathematics. (If you are interested in mathematics, this is your day!)

Nines

When I was a nine, my family took a long drive to the mountains to visit my maternal grandmother. I don’t have any photos, but this picture gives a good idea:

Image courtesy of Google Maps

At nine years old, I was always carsick, and the end of the trip was a definite relief. But even after getting out of the car, the driveway was tilted precariously, and pushing up to get to the slope took me past curious potted cacti cluttering the porch. The sunlight was bright, and the smells of strange animals and stranger cooking always lingered in the house.

But what sticks with me more than anything was something my mother showed me there on the patio using a calculator. Maybe you’ve seen it as well:

\(\frac{1}{9}=0.\overline{1}\)

\(9 \times \frac{1}{9} = 0.\overline{1} \times 9\)

\(1 = 0.\overline{9}\)

This was totally mind-blowing to me at the time. But I thought about it, and even though I didn’t have good mathematical notation, it seemed to imply something about nines. One minus a tenth is 0.9. One minus a hundredth is 0.99. One minus a thousandth is 0.999. So one minus an infinitieth is .9 repeating; the infinitieth is basically zero; it doesn’t matter. Putting it a bit more formally gives something like this:

\(1 - 10^{-1} = 0.9\)

\(1 - 10^{-2} =0.99\)

\(1-10^{-3} =0.999\)

\(1-10^{-\infty} = 0.\overline{9}\)

Now anyone trained in mathematics may well think they have immediately spotted a serious flaw in this reasoning: I’m putting infinity in the exponent position, treating it as a number. Clearly, everyone knows infinity is not a real number. This is not even seriously contestable.

Fine, fine, sure! Infinity is not a real number. But let’s just stick to real numbers and talk about square roots for a little bit, and then see how you feel!

Square Roots, Sticking to Real Numbers

Well now everyone who knows anything knows that “The square root of a number is that thing you need to multiply by itself to get the original number.” So like, the square root of 4 is 2.

Now this is also wrong, in the strictest sense, but it’s at least close, because 2 is definitely a square root of 4. It’s just not the only root; -2 is also a square root of 4. The only real number that has only one square root is 0, because the square root of 0 is just 0.

But what about real numbers less than zero, like -1?

Well again anyone who knows anything will immediately tell you that’s easy: “The square root of -1 is i.”

And now I can’t really tell if you want me to stick to real numbers at all, because i is clearly imaginary. You can’t take the square root of -1 if you’re going to stick to real numbers. It can’t be done; there is no real square root of -1.

And yet imaginary numbers are pretty useful for actual things in the real world, because if you want to use the Schrödinger Equation to describe the time evolution of a quantum state, then you’ve got:

There’s even an entire branch of mathematics out there called Complex Analysis that’s all about imaginary numbers. One of my favorite things in Complex Analysis is called the Riemann Sphere.

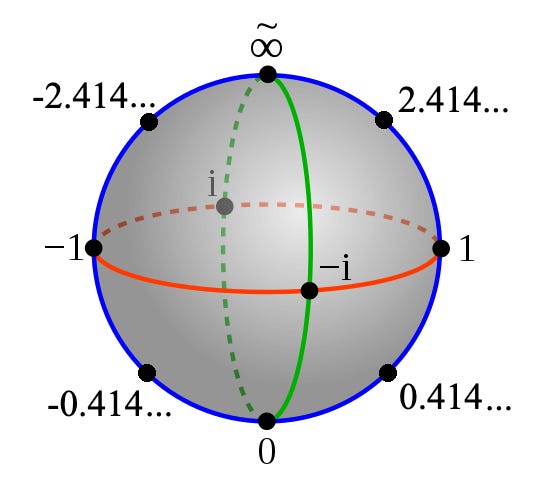
The Riemann Sphere

I think most people have a lot of trouble conceptualizing numbers because they always want to put them on a number line. Very, very useful to thinking about numbers is this thing:

As you can see, the Riemann Sphere doesn’t just have real numbers. It’s got all the real, imaginary, and transfinite numbers in one diagram. At the bottom is zero, the smallest number; in a horizontal ring halfway up we have 1, i, -1, and -i; then at the top we have complex infinity, which is basically a number including positive, negative, and imaginary infinities—anything that’s infinitely big. Indeed, all the big numbers (well, bigger than 1) are found in the upper area. Numbers smaller than 1 are found in the bottom half. To get imaginary numbers, you move into or out of the screen, but the reals are all contained right along the blue ring at the outside of the diagram.

One of the cool things about the Riemann Sphere is that it allows us to visualize simple arithmetic transformations. Just like with the number line, if you want to flip a number’s sign, you just move horizontally across to the opposite side of the sphere. Right? Going from -1 to +1 means moving across to the other side. And flipping the sign on 0 does nothing, because it’s already in the middle—you can’t move horizontally from 0.

But also very nice, and something you can’t do with the number line, is to take a reciprocal: you just move across the Riemann Sphere vertically. All the big numbers on the upper half have a reciprocal on the bottom half, right? 2.414 is the reciprocal of 0.414. Or start with 1 or -1 and take the reciprocal, and you’ll see that they’re already in the middle, vertically speaking—you can’t move vertically from -1 or 1.

And of course we see that 0 and infinity are nice reciprocals also, so,

\(\frac{1}{0} = \tilde{∞}\)

Just as -1 has a square root if you are willing to include i in your space of numbers, zero has a reciprocal if you’re willing to consider the infinities in your space of numbers. In other words, the only thing stopping you from dividing by zero is that you’re putting positive infinity, negative infinity, imaginary infinity, all infinities outside the space of possible solutions to the problem.

To be fair, horses aren’t very good at math, either

Apple Pie, You’re Pulling Our Leg

I am not.

Bill Shillito has an entire website where you can read more about this. Or you can check the Wikipedia article on Riemann Sphere. Or IDK you can see this meme:

But what I hope you might take away from this are more general lessons.

For one thing, if you wall off your space of possibilities, many problems in life will seem to have no solutions. I’m not suggesting this is always wrong. Sometimes you’ll truncate your solution space because you’re refusing to do things that are unethical, or risky, or will cause problems in the long term. But I’ve also seen people tie themselves into knots to avoid having to leave their house, or quit a job, or dump a girlfriend. Sometimes the obvious answer is, well, not so obvious.

But more seriously, I really wish more rationalists people would look at situations like this and realize that they spent years thinking division by zero is impossible. It’s a very rare fellow who wasn’t ever told 1 / 0 = stop doing that. Most people who bother to say anything on the subject at all don’t know that you can live in a space where division by zero is impossible, but you don’t have to. They just insist it’s impossible, and that’s it. Then if they do find out it’s possible to divide by zero under some circumstances, they just think, “Huh, so I guess you can divide by zero in some circumstances,” not “Wow, people spend most of their time wrong about things, I’d better hedge more often.” I know, people don’t really like to hedge, but no one has ever hedged with me about division by zero. What they tell me is “You can’t do that,” with full confidence.

The Lesson

If you’re going to learn a lesson from these kinds of things, the real lesson—the best lesson—is, You don’t know things, Stop assuming you know things, and Hedging is better than being totally wrong.